Appunti nuovi

Calcolo combinatorio

Quali problemi riesce a risolvere il calcolo combinatorio?

Consideriamo un insieme di $n$ oggetti di cui ne seleziono $k$ secondo un determinato criterio. Quanti sono i raggruppamenti formati da $k$ oggetti presi dagli $n$ oggetti originari in modo tale che soddisfino quel determinato criterio?

Esempio Consideriamo la parola “matematica”, quanti anagrammi posso formare considerando che al primo posto devo avere una vocale e alla fine una consonante?

Di questa tipologia di problemi, se ne occupa il calcolo combinatorio.

Disposizioni senza ripetizioni

Definizione

Consideriamo $n$ oggetti distinti Si chiama disposizione semplice un raggruppamento ordinato di $k$ elementi presi dagli $n$ oggetti con $n > k$ .

Cosa vuol dire raggruppamento ordinato? Un raggruppamento differisce dall’altro o per almeno un elemento o anche per l’ordine.

Esempio Consideriamo l’insieme $A = {a, b, c}$ Quanti sono i possibili raggruppamenti a due elementi scelti tra i elementi? Quanti e quali sono le disposizioni (i raggruppamenti)?

$n = 3$ $n = 2$

Ho $6$ raggruppamenti:

(a, b), (a, c), (b, c), (b, a), (c, a), (c, b)

In ciascun raggruppamento, un elemento può figurare in al più una volta.

Ovviamente, non sempre è possibile contare esplicitando tutti i vari raggruppamenti perché $n$ può essere un numero molto grande. Quindi è necessario trovare una formula che generalizzi questo tipo di calcolo.

Info

$D_{n_{k}} = n \cdot (n - 1) \cdot \dots \cdot (n - k + 1)$

Applichiamo la relazione: $D_{3_{2}} = 3 \cdot 2 = 6$

Esempio $n = 9$ $k = 5$

D_{9_{5}} = 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 = 15120

Disposizioni con ripetizioni

Definizione

Si chiamano disposizioni con ripetizione di $n$ elementi a $k$ a $k$ , un gruppo “ordinato” formato con $k$ degli $n$ elementi dove uno stesso elemento può figurare nel gruppo fino a $k$ volte ( $k \geq n$ )

Facciamo riferimento all’esempio precedente:

$A = {a, b, c}$ $n = 3$ $k = 2$

Sta volta, però, se vogliamo ottenere delle disposizioni senza ripetizioni, si devono aggiungere altre coppie.

(a, b), (a, c), (b, c), (b, a), (c, a), (c, b)

Questi sono tutti i raggruppamenti di due elementi che non vengono ripetuti più di una volta. Dato che stiamo considerando le disposizioni con ripetizione, ciascun elemento in qualsiasi raggruppamento, può figurare fino a $k$ volte.

Quindi dobbiamo aggiungere le coppie:

(a, a), (b, b), (c, c)

Quindi le disposizioni finali saranno:

(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)

Per un totale di $9$ raggruppamenti.

Relazione

Numero di disposizioni senza ripetizione di $n$ elementi presi a $k$ a $k$ :
$D_{n_{k}}^{r} = n^{k}$

Utilizzando l’esempio precedente applichiamo la relazione

D_{3_{2}}^{r} = 3^{2} = 9

Esercizio 1

Esercizio 2

Combinazioni semplici

Definizione

Siano $n$ e $k$ due numeri naturali con $n \geq k$ . Si definisce combinazione semplice un raggruppamento di non ordinato di $k$ elementi estratti da un insieme di partenza di $n$ elementi

Consideriamo un insieme $A = {a, b, c}$ . Voglio effettuare dei raggruppamenti di due elementi presi dall’insieme. Le scelte saranno inferiori rispetto alle disposizioni perché non si deve tenere conto dell’ordine.

{a, b}, {a, c}, {b, c}

Relazione

Numero di raggruppamenti formato da $k$ elementi a partire dagli $n$ dati:
$C_{n_{k}} = (k n) = \frac{n !}{k ! \cdot ( n - k )!}$

Seguendo l’esempio:

C_{3_{2}} = (2 3) = \frac{3 !}{2 ! \cdot ( 3 - 2 )!} = \frac{3 \cdot 2 \cdot 1}{( 2 \cdot 1 ) \cdot 1} = \frac{6}{2} = 3

Combinazioni con ripetizione

Definizione

Dati $n$ elementi distinti, si definisce combinazione con ripetizione, un raggruppamento non ordinato di $k$ elementi estratti da un insieme di partenza di $n$ oggetti, dove uno stesso elemento può figurare nel raggruppamento fino a $k$ volte

Prendiamo in esame l’esempio precedente:

$A = {a, b, c}$

$n = 3$

$k = 2$

{a, b}, {a, c}, {b, c}

Dobbiamo aggiungere le coppie

{a, a}, {b, b}, {c, c}

Quindi avremo

{a, a} {a, b}, {a, c}, {b, b}, {b, c}, {c, c}

Per un totale di $6$ raggruppamenti

Relazione

Numero di raggruppamenti formato da $k$ elementi a partire dagli $n$ dati:
$C_{n_{k}}^{r} = (k n + k - 1)$

Seguendo l’esempio di prima:

C_{3_{2}}^{r} = (2 4) = \frac{4 !}{2 ! \cdot ( 4 - 2 )!} = \frac{4 \cdot 3 \cdot 2}{4} = 6

Warning

Nelle combinazioni non è importante l’ordine in cui compaiono gli elementi (altrimenti si tratterebbe di disposizioni). E’ importante sapere “chi c’è” nel gruppo di $k$ elementi, quindi quanti sono i possibili sottoinsiemi di $k$ elementi presi da un gruppo di partenza di $n$

Permutazioni semplici

Supponiamo di avere tre palline $P_{1}, P_{2}, P_{3}$ . Chiaramente potrei cambiare l’ordine delle palline e ordinarle in questo modo:

P_{2}, P_{3}, P_{1}

Questo non è l’unico modo che abbiamo per cambiare l’ordine delle palline. Se si decidesse di scrivere tutte le sequenze ordinate che si possono ottenere con le tre palline otterremmo:

P_{1}, P_{2}, P_{3} P_{1}, P_{3}, P_{2} P_{2}, P_{1}, P_{3} P_{2}, P_{3}, P_{1} P_{3}, P_{1}, P_{2} P_{3}, P_{2}, P_{1}

Informalmente, possiamo considerare ciascuna di queste $6$ come una permutazione delle $3$ palline.

Definizione

Dato un gruppo di elementi $n$ distinti, si definisce permutazione semplice una sequenza ordinata degli $n$ oggetti

Oss: due permutazioni sono diverse se è diverso l’ordine in cui compaiono gli oggetti

Supponiamo di dover capire in quanti modi possiamo riordinare $6$ oggetti. L’oggetto da mettere al primo posto possiamo sceglierlo in $6$ modi. Dato che ci rimangono $5$ oggetti possiamo scegliere in $5$ modi l’oggetto da mettere al secondo posto e così via…

Quindi, quanti modi abbiamo per decidere in che ordine mettere gli oggetti?

6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 6!

Relazione

Numero di modi che abbiamo per realizzare una sequenza ordinata di $n$ oggetti distinti:
$P_{n} = n \times (n - 1) \times (n - 2) \times \dots \times 1 = n!$

Esempio Quanti anagrammi posso formare con la parola $E L I S A$ ? $n = 5$ Quindi:

P_{n} = 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120

Quante permutazioni posso ottenere se voglio avere delle consonanti al primo e all’ultimo posto?

Poniamo il caso di “fissare” la $L$ al primo posto e la $S$ all’ultimo:

L___S

Internamente, le vocali sono $3$ e le posso ordinare in qualsiasi modo. Quindi:

P_{3} \cdot 2 = 3! \cdot 2 = 12

Quante permutazioni posso ottenere se voglio avere delle vocali al primo e all’ultimo posto?

Poniamo il caso di “fissare” la $E$ al primo posto e la $I$ all’ultimo:

E___I

Le rimanenti lettere possono permutare.

Informalmente possiamo dividere la parola in 3 blocchi:

Primo (P) Intermedio (I) Ultimo (U)

Scelta primo carattere Sappiamo che deve essere una vocale e le vocali “disponibili” sono $E, I, A$ . Quindi ho $3$ scelte per il primo posto

Scelta ultimo carattere Anche l’ultima lettera deve essere una vocale, ma una vocale è già stata usata nel primo posto (quindi ne rimangono $2$ ). Perciò, ho $2$ scelte per l’ultimo posto.

Scelta delle lettere intermedie Dopo aver scelto le vocali per primo e ultimo posto, restano 3 lettere (tra consonanti e vocali non usate). Queste possono essere disposte in $3! = 6$ modi

Quindi:

P_{n} = Scelte prima vocale 3 \times Permutazioni lettere intermedie 3! \times Scelte ultima vocale 2 = 3 \cdot 6 \cdot 2 = 36

Formalmente possiamo vedere questa soluzione come le permutazioni per ottenere le lettere intermedie moltiplicate alle disposizioni semplici per ottenere le due vocali all’inizio e alla fine:

$n = 3$

$k = 2$

P_{t o t} P_{t o t} = P_{n} \cdot D_{n_{k}} = 3! \cdot 3 \cdot 2 = 36

Permutazioni con ripetizione

Definizione

Sia A un insieme costituito da $n$ elementi alcuni dei quali si ripetono un certo numero di volte: $A = {si ripete k_{1} volte a_{1}, a_{1}, \dots, a_{1}, si ripete k_{2} volte a_{2}, a_{2}, \dots, a_{2}, a_{m}, si ripete k_{m} volte a_{m}, a_{m}, \dots, a_{m}, b_{1}, b_{2}, b_{r}}$

Quante sono le permutazioni in cui nell’insieme figurano elementi ripetuti?
$P_{n}^{r} = \frac{n !}{k _{1} ! \times k _{2} ! \times \dots \times k _{m} !}$
Dove $k_{1}, k_{2}, \dots, k_{m}$ sono i fattori correlati agli elementi ripetuti

Esempio Voglio costruire tutti i possibili anagrammi con la parola $SISSI$ . $n = 5$ La $I$ si ripete $2$ volte, mentre la $S$ si ripete $3$ volte, quindi $k_{1} = 2$ $k_{2} = 3$

Applicando la relazione otterremo:

P_{n}^{r} = \frac{5 !}{2 ! \cdot 3 !} = \frac{5 \cdot 4 \cdot 3 \cdot 2}{2 \cdot 3 \cdot 2} = 10

Probabilità

Definizioni

Si chiama prova l’esecuzione di un esperimento. Da questa prova si ottiene un risultato.

Per esempio se lancio un dado a 6 facce, eseguo una prova e si ottiene un risultato elementare

Spazio di probabilità

L’insieme formato da tutti i possibili risultati elementari è detto spazio di probabilità o campionario $S$ .

Nel caso del dado, lo spazio di probabilità è $S = {1, 2, 3, 4, 5, 6}$ .

Evento

E’ chiamato evento $E$ un sottoinsieme t.c $E \subseteq S$ di possibili risultati.

evento elementare: se è un insieme composto da un solo elemento

$S = {1, 2, 3, 4, 5, 6}, E = {Esce il numero 3}$ è un evento elementare

evento non elementare: se è un insieme composto da più di un elemento

$S = {1, 2, 3, 4, 5, 6}, E = {Esce un numero maggiore di 5}$

evento impossibile: se l’insieme è vuoto

$S = {1, 2, 3, 4, 5, 6}, E = {Esce il numero 7}$

evento certo: se l’insieme coincide con $S$

$S = {1, 2, 3, 4, 5, 6}, E = {Esce un numero compreso tra 1 e 6}$

Evento prodotto, evento somma e evento differenza

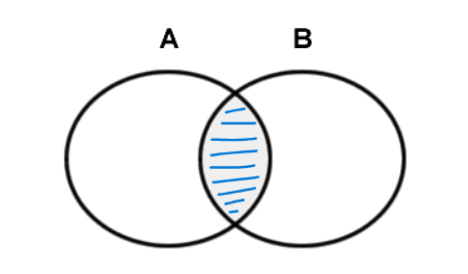
Evento prodotto

Siano $A$ e $B$ due eventi, l’evento prodotto $A \cap B$ , l’evento che consiste nel realizzarsi contemporaneamente sia $A$ che $B$ .

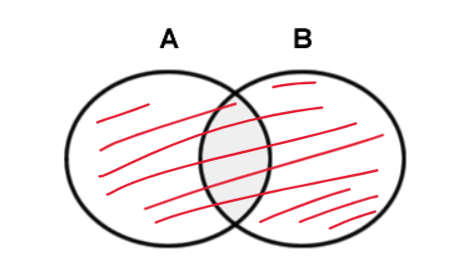
Evento somma

Siano $A$ e $B$ due eventi, l’evento prodotto $A \cup B$ , l’evento che consiste nel realizzarsi o di sia $A$ o di $B$ .

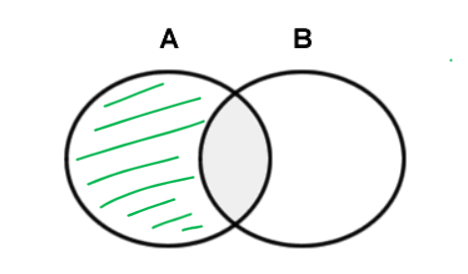
Evento differenza

Siano $A$ e $B$ due eventi, l’evento prodotto $A ∖ B$ , l’evento che consiste nel realizzarsi di $A$ ma non di $B$ .

Evento complementare

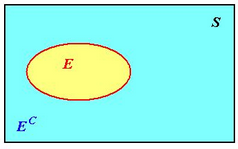
Definizione

Sia $S$ lo spazio delle probabilità e sia $E$ un evento t.c. $E \subseteq S$ . Si definisce evento complementare $\overline{E}$ o $E^{c}$ , l’evento costituito da tutti gli eventi elementari di $S$ che non appartengono a $E$ .

Esempio Lancio un dado $S = {1, 2, 3, 4, 5, 6}$ e considero $E = {2, 4, 6}$ , il complementare di $E$ sarà $E^{c} = {1, 3, 5}$ .

Eventi incompatibili

Definizione

Due eventi sono incompatibili se non possono realizzarsi contemporaneamente.

Probabilità

Definizione

Sia $E$ un evento aleatorio risultato di un certo esperimento. Si definisce probabilità di $A$ il rapporto di casi favorevoli e il numero di casi possibili.
$P (E) = \frac{n _{F}}{N _{T}}$

Assiomi della probabilità

Assioma 1

$P (E) \in [0, 1] \forall E \subset S$

Assioma 2

$P (S) = 1$

Assioma regola del prodotto

Data una successione $E_{1}, E_{2}, \dots, E_{n}$ eventi a 2 a 2 disgiunti (incompatibili) vale:
$P (i = 1 ⋃ \infty E_{i}) = i = 1 \sum \infty P (E_{i})$

Proposizioni della probabilità

Probabilità dell'evento impossibile

$P (\emptyset) = 0$

Probabilità dell'evento complementare

Consideriamo un evento $E$ , la probabilità del suo evento complementare $E^{c}$ sarà:
$P (E^{c}) = 1 - P (E) \forall E \subset S$

Monotonia della funzione di probabilità

Dati due eventi $F$ e $E$ tale che $E \subset F$ , vale che:
$P (F) \leq P (E)$

Principio di inclusione/esclusione

Due eventi:
$P (A \cup B) = P (A) + P (B) - P (A \cap B)$
Tre eventi:
$P (A \cup B) = P (A) + P (B) + P (C) - P (A \cap B) - P (A \cap C) - P (B \cap C) + P (A \cap B \cap C)$

Esempio Lancio un dado a 12 facce, qual è la probabilità che esca un numero pari?

$S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}$ $E = {2, 4, 6, 8, 10, 12}$

P (E) = \frac{# di numeri pari}{# di numeri totali nel dado} = \frac{6}{12} = \frac{1}{2}

Qual è la probabilità che esca un multiplo di $3$ ?

$S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}$ $F = {3, 6, 9, 12}$

P (F) = \frac{4}{12} = \frac{1}{3}

Qual è la probabilità dell’evento somma?

In questo caso devo considerare l’evento $E \cup F$ . $E \cup F = {2, 3, 4, 6, 8, 9, 10, 12}$

P (E \cup F) = \frac{8}{12} = \frac{2}{3}

Possiamo anche ottenerla con il principio di inclusione esclusione:

P (E \cup F) P (E \cup F) = P (E) + P (F) - P (E \cap F) = \frac{1}{2} + \frac{1}{3} - \frac{1}{6} = \frac{2}{3}

Probabilità condizionata

Eventi dipendenti e indipendenti

Definizioni

Due eventi si definiscono dipendenti se il fatto che si verifichi (o meno) il primo, altera la probabilità che si verifichi il secondo

Due eventi si definiscono indipendenti se il fatto che si verifichi (o meno) il primo, non altera la probabilità che si verifichi il secondo

Esempio Qual è la probabilità che lanciando un dado e una moneta si ottengano un 4 e una testa?

Gli esiti possibili sono:

$E = {Escono un 4 e una test}$

P (E) = \frac{casi favorevoli}{casi possibili} = \frac{1}{12}

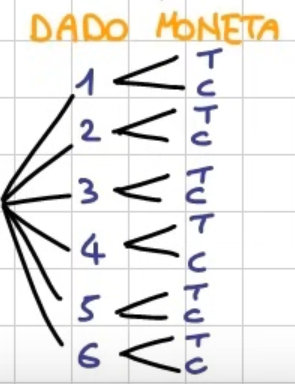
Da notare che la probabilità di ottenere un $4$ è $\frac{1}{6}$ e la probabilità di ottenere una testa è $\frac{1}{2}$ . Quindi $\frac{1}{12}$ non è altro che il prodotto tra $\frac{1}{2}$ e $\frac{1}{6}$ . In particolare, la probabilità di ottenere un 4 e una testa non è altro che la probabilità di ottenere un 4 moltiplicata alla probabilità di ottenere una testa.

Ma i due eventi sono dipendenti o indipendenti? Per capirlo si deve pensare se il risultato che si ottiene con il dado influenza o meno quello che si ottiene lanciando la moneta. Chiaramente, non c’è alcun motivo di ritenere che il dado modifichi la probabilità di uscita della testa con la moneta. Perciò, i due eventi sono indipendenti.

Info

Quindi se $A$ e $B$ sono eventi indipendenti, allora:
$Probabilit \overset{a}{ˋ} che si verifichino entrambi P (A \cap B) = Probabilit \overset{a}{ˋ} che si verifichi A P (A) \times Probabilit \overset{a}{ˋ} che si verifichi B P (B)$

Esempio In una classe ci sono $20$ alunni, di cui $12$ femmine e $8$ maschi. La professoressa sceglie a caso $2$ alunni da interrogare. Qual è la probabilità che scelga $2$ ragazze?

$E = {2 ragazze interrogate}$

P (E) = \frac{( 2 12 )}{( 2 20 )} = \frac{12 \cdot 11}{20 \cdot 19}

Immaginiamo di aver fatto la scelta in successione. Qual è la probabilità che venga scelta una ragazza al primo colpo?

P (F) = \frac{12}{20}

La probabilità di scegliere un’altra ragazza è:

P (G) = \frac{11}{19}

Questo perché dopo aver fatto la prima scelta, gli alunni che rimangono sono $19$ e le ragazze $11$ . Quindi possiamo dire che:

P (E) = \frac{( 2 12 )}{( 2 20 )} = Probabilit \overset{a}{ˋ} di scegliere una ragazza \frac{12}{20} \times Probabilit \overset{a}{ˋ} di scegliere una ragazza sapendo che ne ho gi \overset{a}{ˋ} scelta una prima \frac{11}{19}

Quindi la probabilità $P (G)$ dipende da $P (F)$ .

Definizione

Se $A$ e $B$ sono due eventi dipendenti:
$P (A \cap B) P (A ∣ B) = P (A) \cdot P (B ∣ A) = \frac{P ( A \cap B )}{P ( B )}$
Dove: $P (A \cap B) = probabilit \overset{a}{ˋ} che si verifichino entrambi gli eventi$ $P (A) = probabilit \overset{a}{ˋ} che si verifichi A$ $P (A ∣ B) = probabilit \overset{a}{ˋ} che si verifichino l’evento B sapendo che si \overset{e}{ˋ} verificato l’evento A$

Probabilità totale

Supponiamo di avere $3$ contenitori uguali contenenti delle palline nel seguente modo: $I = {5 nere, 3 blu, 2 rosse}$ $II = {1 verde, 9 blu, 7 rosse}$ $III = {2 nere, 8 blu}$

Sapendo che la probabilità di scelta delle scatole siano uguali (è equiprobabile) $P (I) = P (II) = P (III)$ , qual è la probabilità $P (E)$ di selezionare una pallina nera?

Probabilità totale

$P (A) = i = 1 \sum n P (E_{i}) \cdot P (A ∣ E_{i})$

Quindi, tornando all’esempio precedente applichiamo la formula della probabilità totale.

P (E) = P (I) \cdot P (E ∣ I) + P (II) \cdot P (E ∣ II) + P (III) \cdot P (E ∣ III) = \frac{1}{3} \cdot \frac{5}{10} + \frac{1}{3} \cdot \frac{0}{17} + \frac{1}{3} \cdot \frac{2}{10} = \frac{7}{30}

Teorema di Bayes

Prendiamo in riferimento l’esempio delle $3$ scatole. $I = {5 nere, 3 blu, 2 rosse}$ $II = {1 verde, 9 blu, 7 rosse}$ $III = {2 nere, 8 blu}$ $P (E) = {Probabilit \overset{a}{ˋ} di estrarre una pallina nera} = \frac{7}{30}$

Ma, qual è la probabilità che la pallina estratta sia stata estratta dalla prima scatola?

Formula di Bayes

$P (E ∣ A) = \frac{P ( E ) \cdot P ( A ∣ E )}{P ( A )}$

$P (I ∣ E)$ = $Probabilit \overset{a}{ˋ} di aver scelto una pallina nera dalla prima scatola$ Applichiamo la formula di Bayes:

P (I ∣ E) = \frac{P ( I ) \cdot P ( E ∣ I )}{P ( E )} = \frac{\frac{1}{3} \cdot \frac{5}{10}}{\frac{7}{30}} = \frac{5}{7}

Variabili aleatorie

Variabili aleatorie discrete

Supponiamo che un docente voglia sapere quanti alunni sono previsti per la lezione di domani. Ovviamente non possiamo saperlo a priori, ma possiamo porci delle domande.

Qual è la probabilità che si presenteranno 100 studenti?

Oppure

Qual è la probabilità che si presenteranno 90 studenti?

Il numero di studenti rappresenta il valore assunto dalla variabile aleatoria $X$ .

Definizione

Siano $S$ lo spazio campionario e $T$ un insieme numerico. Si definisce variabile aleatoria discreta $X$ una funzione che mette in corrispondenza ogni elemento di $S$ con un elemento di $T$ .
$X : S \to T$

Esempio Supponiamo di avere due monete, una rossa e una blu. Sulla faccia di ogni moneta è riportato il numero 1 o il numero 2 (la moneta blu ha una faccia con il numero 1 e l’altra con il numero 2 e stessa cosa la moneta rossa). Lancio contemporaneamente le due monete e ottengo i seguenti risultati:

(1 B, 1 R) (1 B, 2 R) (2 B, 1 R) (2 B, 2 R)

Questi sono tutti gli eventi elementari che compongono $S$ . Ora decido che a ogni risultato venga associato un numero dato dalla somma dei valori della coppia.

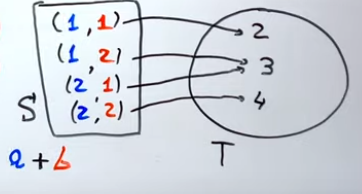
Ognuno di questi valori si può presentare con una determinata probabilità. La variabile aleatoria $X$ può assumere i seguenti valori

X = 2 X = 3 X = 4

Qual è la probabilità che la variabile aleatoria assuma come valore $2$ ?

Questo equivale a dire, qual è la probabilità che esca la coppia $(1, 1)$ ?

P (E) = ⎩ ⎨ ⎧ \frac{1}{4} X = 2 \frac{1}{3} X = 3 \frac{1}{4} X = 4

Valore atteso e Varianza

Valore atteso $X$ una variabile aleatoria discreta che assume valori $x_{1}, x_{2}, \dots, x_{n}$ ognuno con probabilità $P_{1}, P_{2}, \dots, P_{n}$ . Il valore atteso $E (X)$ della variabile aleatoria è dato da:

Sia

$E [X] = x_{1} \cdot P_{1} + x_{2} \cdot P_{2} + \dots + x_{n} \cdot P_{n}$

Proprietà

$E [a X + b] = a \cdot E [X] + b$

$E [a X + bY + c] = a \cdot E [X] + b \cdot E [Y] + c$

Varianza

Sia $X$ una variabile aleatoria discreta che assume valori $x_{1}, x_{2}, \dots, x_{n}$ ognuno con probabilità $P_{1}, P_{2}, \dots, P_{n}$ . La varianza $V (X)$ della variabile aleatoria è dato da:
$Va r (X) = E [(X - valore atteso EX)^{2}] = (x_{1} - E)^{2} \cdot P_{1} + (x_{2} - E)^{2} \cdot P_{2} + \dots + (x_{n} - E)^{2} \cdot P_{n}$

Calcolo alternativo della varianza

E’ possibile calcolare la varianza anche come;
$Va r (X) = E [X^{2}] - (EX)^{2}$

Proprietà

$Va r (a X + b) = a^{2} \cdot Va r (x)$

$Va r (x + y) = Va r (X) + Va r (Y) + 2 \cdot C o v (X, Y)$

$Va r (X + Y + Z) = Va r (X) + Va r (Y) + Va r (Z) + 2 \cdot C o v (X, Y) + 2 \cdot C o v (X, Z) + 2 \cdot C o v (Y, Z)$

Scarto quadratico medio o deviazione quadratica

La deviazione quadrata di una variabile aleatoria è una misura della dispersione dei valori della variabile rispetto al suo valore medio.

Non è altro che una misura più intuitiva della dispersione rispetto alla varianza, poiché è espressa nella stessa unità di misura della variabile aleatoria.

Sia $X$ una variabile aleatoria discreta, la deviazione quadrata di X è definita come:
$σ (X) = Va r (X) = E [(X - EX)^{2}]$

Prendiamo in considerazione l’esempio delle due monete.

$S = {(1 B, 1 R), (1 B, 2 R), (2 B, 1 R), (2 B, 2 R)}$ $X = a + b = {2, 3, 4}$

P (E) = ⎩ ⎨ ⎧ \frac{1}{4} X = 2 \frac{1}{3} X = 3 \frac{1}{4} X = 4

Calcoliamo il valore medio:

E (X) = 2 \cdot \frac{1}{4} + 3 \cdot \frac{1}{3} + 4 \cdot \frac{1}{4} = 3

Calcoliamo la varianza:

Va r (X) = (2 - 3)^{2} \cdot \frac{1}{4} + (3 - 3)^{2} \cdot \frac{1}{3} + (4 - 3)^{2} \cdot \frac{1}{4} = \frac{1}{2}

E la deviazione quadratica è:

σ (X) = \frac{1}{2}

Distribuzione binomiale

Supponiamo di condurre un certo numero di esperimenti $e_{1}, e_{2}, \dots, e_{n}$ . Ogni esperimento da luogo a due eventi: $A$ e $A^{c}$ .

Su $n$ esperimenti, qual è la probabilità che si abbia un certo numero $X$ di successi?

Lancio una moneta $20$ volte. Qual è la probabilità che su $20$ lanci, esca $9$ volte testa?

Info

La probabilità di ottenere $k$ successi in $n$ prove è data dalla formula:
$P (X = k) = (k n) \cdot p^{k} \cdot (1 - p)^{n - k}$
Dove $p$ è la probabilità che si verifichi l’evento $A$ .

Esempio Lancio una una moneta $5$ volte, qual è la probabilità che testa esca esattamente $4$ volte?

$n = 5$ $k = 4$ $p = P (T) = \frac{1}{2}$

P (X = 4) = (4 5) \cdot (\frac{1}{2})^{4} \cdot (1 - \frac{1}{2})^{5 - 4} = \frac{5}{32}

Determinare la probabilità che testa esca almeno $4$ volte. Questo significa che testa può uscire anche $5$ volte.

P (X \geq 4) = P (X = 5) + P (X = 4) = (5 5) \cdot (\frac{1}{2})^{5} \cdot (1 - \frac{1}{2})^{0} + \frac{5}{32} = \frac{6}{32}

Determinare la probabilità che testa esca almeno una volta. Posso determinare la probabilità che testa non esca mai e calcolo il complementare.

P (X = 0) = (0 5) \cdot (\frac{1}{2})^{0} \cdot (1 - \frac{1}{2})^{5 - 0} = \frac{1}{32}

P (X \geq 1) = 1 - P (X = 0) = 1 - \frac{1}{32} = \frac{31}{32}

Varianza e valore atteso

$E (X) = n \cdot p Va r (X) = n \cdot p \cdot (1 - p)$

Distribuzione di Bernoulli

Una variabile di Bernoulli è una variabile aleatoria che può assumere solo due valori possibili, solitamente indicati come $0$ e $1$ , o come “successo” e “insuccesso”.

Definizione

Una variabile aleatoria $X$ è detta di Bernoulli di parametro $p \in [0, 1]$ se:
$P (X = 1) = p P (X = 0) = 1 - p$

Oss

$E [X] = p$

$E [X^{2}] = p$

$Va r (X) = p \cdot (1 - p)$

Distribuzione binomiale negativa

La variabile aleatoria binomiale negativa rappresenta il numero di prove necessarie per ottenere un certo numero di successi, dove ogni prova ha una probabilità costante di successo e l’ultima prova deve essere un successo.

Un giocatore tira un dado finché ottiene $3$ successi (cioè 3 volte esce 6). Qual è la probabilità che il terzo $6$ esca esattamente al settimo lancio?

Info

Indichiamo una variabile aleatoria binomiale negativa $X$ di parametri $r, p$ con:
$X = B i n^{-} (r, p)$
Dove:

$r$ è il numero di successi desiderati

$p$ è la probabilità di successo in ogni prova

Probabilità

$P (X = k) = (r - 1 k - 1) \cdot p^{r} \cdot (1 - p)^{k - r}$

Valore atteso e varianza

$E [X] = \frac{r}{p} Va r (X) = \frac{r \cdot ( 1 - p )}{p ^{2}}$

Distribuzione geometrica

Una variabile aleatoria geometrica è una variabile aleatoria che rappresenta il numero di prove necessarie per ottenere il primo successo in una sequenza di prove indipendenti, ognuna delle quali ha una probabilità di successo costante.

Notazione

Indichiamo una variabile aleatoria geometrica $X$ di parametro $p$ con:
$X = G eo m (p)$
Dove $p$ indica la probabilità di successo in ogni prova.

Probabilità

La probabilità di ottenere il primo successo alla $k$ -esima prova è data dalla formula:
$P (X = k) = (1 - p)^{k - 1} \cdot p$
oss: $P (k = \infty) = 0$ è la probabilità che non ci sia mai un successo

Valore atteso e varianza

$E [X] = \frac{1}{p} Va r (X) = \frac{1 - p}{p ^{2}}$

Distribuzione ipergeometrica

Una variabile aleatoria ipergeometrica è una variabile aleatoria che rappresenta il numero di successi in una sequenza di prove senza sostituzione, dove ogni prova ha una probabilità di successo costante.

Notazione

Indichiamo una variabile aleatoria ipergeometrica $X$ di parametri $N, K, n$ con:
$X = Hy p (N, K, n)$
Dove:

$N$ è il numero totale di oggetti

$K$ è il numero totale di oggetti “successo”

$n$ è il numero di prove

Probabilità

La probabilità di ottenere $k$ successi in n prove è data dalla formula:
$P (X = k) = \frac{( k K ) \cdot ( n - k N - K )}{( n N )}$

Valore atteso e varianza

$E [X] = \frac{n \cdot K}{N} Va r (X) = n \cdot p \cdot (1 - p) \cdot (\frac{N - n}{N - 1})$
Dove $p = \frac{m}{N}$

Distribuzione di Poisson

Supponiamo di dividere una giornata in intervalli di un’ora. Vogliamo sapere il numero di passeggieri che transitano ai controlli di sicurezza in un aeroporto tra le 8:00 e le 9:00. Qual è la probabilità che i passeggieri siano $1500$ ?

Oppure

Probabilità di trovare un errore di battitura tra le prime $200$ pagine di un libro.

Una variabile aleatoria di Poisson è una variabile aleatoria che rappresenta il numero di eventi che si verificano in un intervallo di tempo o spazio fissato, dove gli eventi sono indipendenti e hanno una probabilità costante di verificarsi.

Notazione

Indichiamo una variabile aleatoria di Poisson $X$ di parametro $λ$ con:
$X = P o i s (λ)$
Dove $λ$ è un parametro positivo e indica la media del numero di eventi che si verificano nell’intervallo di tempo o spazio fissato

Probabilità

La probabilità di ottenere $k$ eventi è data dalla formula:
$P (X = k) = \frac{λ ^{k} \cdot e ^{- λ}}{k !}$
Dove:

$P (X = k) \geq 0 \forall k = 0, 1, 2, \dots$

$\sum_{k = 0}^{\infty} P (X = k) = 1$

Valore atteso e varianza

$E [X] = λ Va r (X) = λ$

Approssimazione di variabile di binomiale con Poisson Se $n$ e molto grande e $p$ molto piccolo, la variabile binomiale $B in (n, p)$ può essere approssimata dalla variabile aleatoria di Poisson con parametro $λ = n \cdot p$

P o i s (n \cdot p) \approx B in (n, p) ⟺ P o i s (λ) \approx B in (n, \frac{λ}{n})

Variabili aleatorie congiunte

Una variabile aleatoria congiunta rappresenta il comportamento di due o più variabili aleatorie correlate.

Notazione

Siano $X, Y$ due variabili aleatorie definite su uno stesso spazio campionario. Indichiamo con $(X, Y)$ la variabile aleatoria congiunta ovvero una funzione che associa ad ogni punto dello spazio campionario un valore della coppia $X, Y$

Probabilità

Date due variabili aleatorie $X, Y$ definite sullo stesso spazio campionario $(X : S \to R e Y : S \to R)$ ed entrambe discrete, dove:

$X$ da valori in ${x_{i}}_{i \in I}$

$Y$ ha valori in ${y_{j}}_{j \in J}$ La densità di probabilità discreta disgiunta $P_{X, Y}$ è la funzione:

$P_{X \times Y} : {x_{i}}_{i \in I} \times {y_{j}}_{j \in J} \to [0, 1]$
Data $P_{X, Y} (x_{i}, y_{j}) = P (X = x_{i}, Y = y_{j})$

Proprietà

$P_{X, Y} (x_{i}, y_{i}) \in [0, 1]$

$\sum_{i \in I} \sum_{j \in I} P_{X, Y} (x_{i}, y_{j}) = 1$

Valore atteso

Siano $X, Y$ variabili aleatorie discrete e sia $f : R^{2} \to R$ , allora:
$E [f (X, Y)] = i \in I \sum j \in I \sum f (x_{i}, y_{j}) P_{X, Y} (x_{i}, y_{j})$
Dove:

${X_{i}}_{i \in I}$ è l’insieme dei possibili valori di $X$

${Y_{j}}_{j \in J}$ è l’insieme dei possibili valori di $Y$

Proprietà somma

$E [X + Y] E [X_{1} + \dots + X_{n}] E [a_{1} X_{1} + \dots + a_{n} X_{n}] = E [X] + E [Y] = E [X_{1}] + \dots + E [X_{n}] = a_{1} E [X_{1}] + \dots + a_{n} E [X_{n}]$
Più in generale dai $a_{1}, a_{2}, \dots, a_{n} \in R$

Proprietà prodotto

Questo vale soltanto se sono indipendenti:
$E [X Y] = E [X] \cdot E [Y]$

Varianza

$Va r (X + Y) = Va r (X) + Va r (Y) \cdot 2 \cdot C o v (X, Y)$

$Va r (f (x) + g (x)) = Va r (f (x)) + Va r (g (x)) \cdot 2 \cdot (f (x), g (x))$

Esempio

Covarianza

Teorema

Date le variabili aleatorie discrete $X, Y : S \to R$ , la covarianza di $X$ e $Y$ è data da:
$C o v (X, Y) = E [X Y] - E [X] \cdot E [Y]$

Proprietà

$C o v (X, X) = Va r (X)$

$C o v (X, Y) = C o v (Y, X)$

$C o v (X, a) = 0 (a costante)$

Se si ha una costante nella covarianza

$C o v (1, 2) = 0$

$C o v (2 X, 3) = 0$

Linearità

$C o v (a X, bY) = a \cdot b \cdot C o v (X, Y)$

$C o v (X, Y) = 0 se X e Y sono indipendenti$

Variabili aleatorie continue

Una variabile aleatoria continua può assumere un qualsiasi valore $X = x$ con $x \in (a, b)$ . L’intervallo $(a, b)$ può essere limitato o illimitato. Quindi, a differenza delle variabili aleatorie discrete che assumono valori discreti, le variabili aleatorie continue possono assumere un qualsiasi valore dell’intervallo $(a, b)$ .

Funzione di probabilità

Una variabile aleatoria $X : S \to R$ è detta continua se esiste una funzione $f : R \to [0, + \infty]$ tale che:
$P (X \in A) = \int_{A} f (x) d x$

Variabili aleatorie continue uniformi

Una variabile aleatoria continua uniforme è una tipologia di variabile aleatoria continua in cui tutti i valori all’interno di un certo intervallo possono presentarsi con probabilità.

Notazione

Variabile aleatoria continua uniforme sull’intervallo $[a, b]$
$X = U ni f ([a, b])$

Funzione di densità

Una variabile aleatoria continua è uniforme sull’intervallo $[a, b]$ se ha come funzione di densità:
$f (x) = ⎩ ⎨ ⎧ \frac{1}{b - a} se x \in [a, b] 0 altrimenti$
oss: $f (x) \geq 0$

Funzione di densità variabile aleatoria continua NON uniforme

Una v.a. continua $X$ non uniforme sull’intervallo $[a, b]$ ha come funzione di densità $f (x)$ che può variare in modo non costante all’interno dell’intervallo. La funzione di densità deve soddisfare le seguenti condizioni:
$f (x) = {g (x) se x \in [a, b] 0 altrimenti$
Dove $g (x)$ è una funzione continua e positiva nell’intervallo $[a, b]$ e soddisfa la condizione di normalizzazione:
$\int_{a}^{b} g (x) d x = 1$
oss: $f (x) \geq 0$

Densità di probabilità sotto-intervallo

La probabilità che la v.a. continua definita su $[a, b]$ assuma un valore in un intervallo $[c, d]$ all’interno di $[a, b]$ è data da:
$P (X \in [c, d]) = \int_{c}^{d} f (x) d x$
Per ogni $a \leq c < d \leq b$ oss:

$P (X \in [a, b]) = 1$

$P (X \in [- \infty, + \infty]) = 1$

Formula semplificata per continue uniformi

Data $X = U ni f ([a, b])$ :
$P (X \in [c, d]) = \int_{c}^{d} f (x) d x = \frac{d - c}{b - a}$

Esercizi

Casi particolari

Densità di probabilità su un intervallo puntiforme

Quando si considera la probabilità che una variabile aleatoria continua X assuma un valore in un singolo punto $x$ , si ha:
$P (X = x) = 0 \forall x \in R$

Densità di probabilità su intervallo parzialmente contenuto

Sia $X$ una variabile aleatoria continua definita sull’intervallo $[a, b]$ .

Quando si calcola la probabilità che $X$ assuma un valore in un intervallo $[c, d]$ che non è completamente contenuto nell’intervallo originale $[a, b]$ , è necessario considerare solo la parte dell’intervallo $[c, d]$ che rientra in $[a, b]$ .

Funzione di distribuzione, valore atteso, varianza e covarianza

La funzione di distribuzione (o ripartizione) è una funzione matematica che descrive la probabilità che una variabile aleatoria assuma valori inferiori o uguali a un certo valore.

Calcolo

Data una variabile aleatoria continua $X$ , la funzione di distribuzione è calcolata:
$F_{X} (b) = P (X < b) = \int_{- \infty}^{b} f (x) d x$
Dove:

$F_{X} (b)$ è la funzione di distribuzione di $X$

$f (x)$ è la funzione di densità di $X$

Valore atteso

Se $X$ è una variabile aleatoria continua, allora:
$E [X] = \int_{- \infty}^{+ \infty} x f (x) d x$
Formula semplificata per le continue uniformi: $E [X] = \frac{a + b}{2}$

Valore atteso funzione di una variabile aleatoria

Sia $X$ una variabile aleatoria con funzione di densità $f$ e sia $g : R \to R$ , allora
$E [g (x)] = \int_{- \infty}^{+ \infty} g (x) f (x) d x$

Proprietà

$X$ variabile aleatoria continua e $a, b \in R$ , allora:

$E [a X + b] = a \cdot E [X] + b$

$X$ variabile aleatoria continua tale che $X_{1}, \dots, X_{n}$ con $a_{1}, \dots, a_{2} \in R$ , allora:

$E [i = 2 \sum n a_{i} X_{i}] = i = 1 \sum n a_{i} E [X_{i}]$

Varianza

Sia $X$ variabile aleatoria continua allora la varianza è:
$Va r (X) = E [(X - E [X]^{2})]$
Formula semplificata per continue uniformi: $Va r (X) = \frac{( b - a ) ^{2}}{12}$

Covarianza

Siano $X$ e $Y$ variabili aleatorie continue:
$C o v (X, Y) = E [(X - E [X]) (Y - E [Y])]$

Distribuzione di Gauss

Una variabile aleatoria gaussiana o normale, è una variabile aleatoria che segue una distribuzione di probabilità normale, anche nota come distribuzione gaussiana.

Questa distribuzione è caratterizzata da una curva a campana simmetrica intorno alla media, con una probabilità maggiore di osservare valori vicini alla media e una probabilità minore di osservare valori più lontani dalla media.

La distribuzione gaussiana è completamente determinata da due parametri:

La media $μ$ rappresenta il valore centrale della distribuzione
La varianza $σ^{2}$ rappresenta la dispersione dei valori intono alla media

Definizione

Una variabile aleatoria $X$ è detta gaussiana (o normale) di media $μ \in R$ e con varianza $σ^{2} > 0$ se è una variabile aleatoria continua con funzione di densità:
$f (x) = \frac{1}{2 π σ} \cdot e^{\frac{- ( x - μ ) ^{2}}{2 σ ^{2}}}$
Se $μ = 0$ e $σ^{2} = 1$ allora $X$ è detta gaussiana standard dove:
$f (x) = \frac{1}{2 π} \cdot e^{- \frac{x ^{2}}{2}}$

Notazione

Una variabile aleatoria $X$ continua gaussiana di media $μ \in R$ con varianza $σ^{2} > 0$ è indicata con:
$X = N (μ, σ^{2})$
oss: $μ = E [x]$ e $σ^{2} = Va r (x)$

Funzione di distribuzione

Sia $X = N (0, 1)$ calcoliamo $F (x)$ , cioè $P (X) = x$

Φ (X) = \frac{1}{2 π} \int_{- \infty}^{x} e^{\frac{( z - μ ) ^{2}}{2 σ ^{2}}} d z

Funzione di distribuzione gaussiana standard

Sia $X = N = (0, 1)$ invece di scrivere $F (X)$ , scriviamo $Φ (x)$ :
$Φ (X) = \frac{1}{2 π} \int_{- \infty}^{x} e^{- \frac{z ^{2}}{z}} d z$
se vogliamo trovare il valore negativo basta fare $Φ (x) = 1 - Φ (x)$ oss: $Φ (x) = P (Z \leq x)$

Proposizione 1

Siano $μ \in R, σ^{2} > 0$ e $Z = N (0, 1)$ , allora:
$Y = \pm σ Z + μ$
Dove possiamo calcolare:

$E [Y] = E [σ Z + μ] = σ E [Z] + μ = σ \cdot 0 + μ = μ$

$Va r (Y) = Va r (σ Z + μ) = σ^{2} \cdot Z \cdot Va r (Z) = σ^{2} \cdot 1 = σ^{2}$

Proposizione 2

$Y = N (μ, σ^{2}) ⟹ \frac{Y - μ}{σ} = N (0, 1)$

👾 Ineffable Notes

Explorer

Appunti nuovi

Calcolo combinatorio

Disposizioni senza ripetizioni

Disposizioni con ripetizioni

Combinazioni semplici

Combinazioni con ripetizione

Permutazioni semplici

Permutazioni con ripetizione

Probabilità

Evento prodotto, evento somma e evento differenza

Evento complementare

Eventi incompatibili

Probabilità

Probabilità condizionata

Eventi dipendenti e indipendenti

Probabilità totale

Teorema di Bayes

Variabili aleatorie

Variabili aleatorie discrete

Valore atteso e Varianza

Distribuzione binomiale

Distribuzione di Bernoulli

Distribuzione binomiale negativa

Distribuzione geometrica

Distribuzione ipergeometrica

Distribuzione di Poisson

Variabili aleatorie congiunte

Covarianza

Variabili aleatorie continue

Variabili aleatorie continue uniformi

Casi particolari

Funzione di distribuzione, valore atteso, varianza e covarianza

Distribuzione di Gauss

Funzione di distribuzione

Graph View

Table of Contents

Backlinks